VOLÚMENES DE SÓLIDOS

MÉTODO DE LAS CAPAS CILÍNDRICAS

Más información

Método de las capas cilíndricas

              En algunos casos se desea calcular el volumen de una región limitada por una función y=f(x) al girar al rededor del eje y, para lo cual se deben hallar los extremos locales de f(x) y despejar x en términos de y (x=g(x)). Esto muchas veces es muy complicado por lo que se utilizará EL MÉTODO DE LAS CAPAS CILÍNDRICAS, el cual facilita encontrar dicho volumen generado por las funciones dadas.

           Es un método de cálculo integral que permite evaluar volúmenes de sólidos de revolución. Consiste en dividir el sólido de revolución en una serie de casquetes cilíndricos que se incrustan los unos dentro de los otros y en integrar luego de los volúmenes de estos casquetes para obtener el volumen total
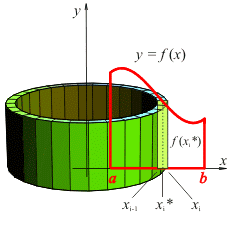
Método de las capas cilíndricas image

DETERMINACIÓN DEL VOLUMEN DE UN CASCARON

A. La arandela o lata se corta por un lado. B. Se aplana olvidando sus tapaderas. C. El resultado es un sólido rectangular.

DETERMINACIÓN DEL VOLUMEN DE UN CASCARON

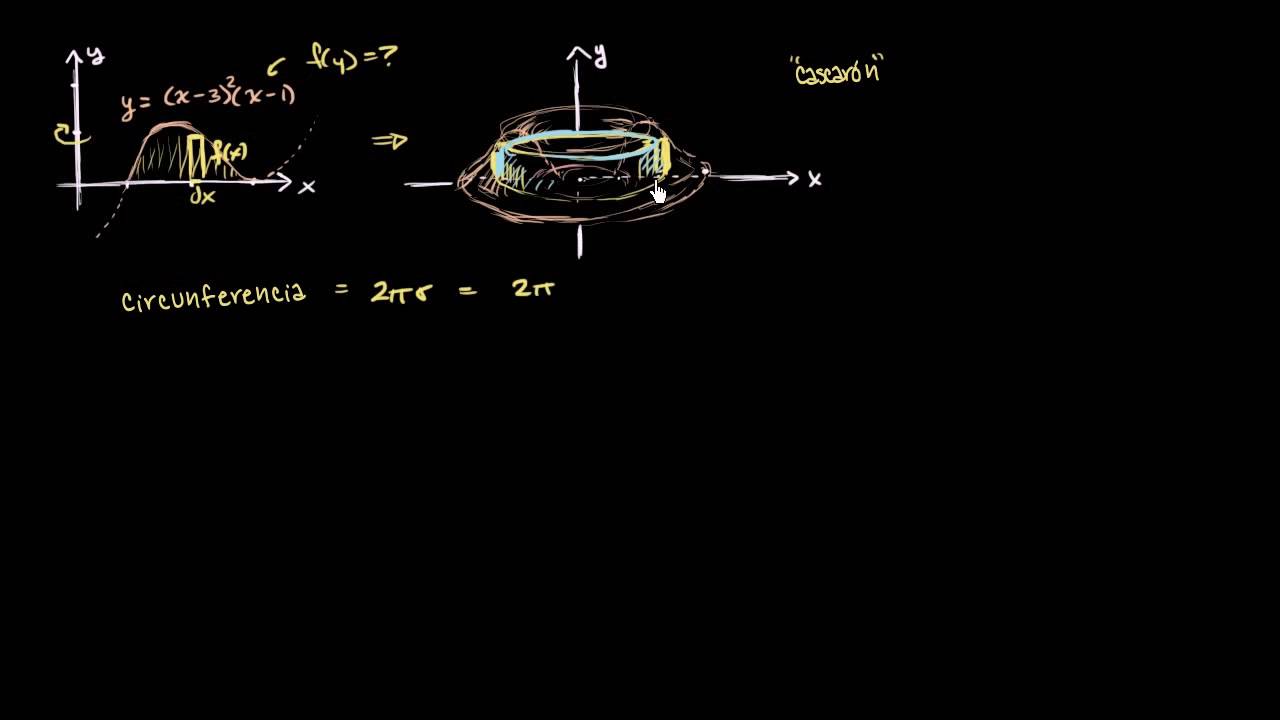
Aprenderemos como usar el método de los cascarones cilíndricos para encontrar el volumen obtenido al rotar el área que se encuentre entre a y b. Lo primero que tenemos que hacer es identificar el método que vamos a utilizar para encontrar el volumen dado. El método de cascarones cilíndricos, para lo cual tomaremos un punto arbitrario en la curva, el cual notaremos como (x,y) y construiremos un elemento de área desde este punto y paralelo al eje de rotación tal y como se muestra en la siguiente figura.

FÓRMULA DE VOLUMEN DE UN SÓLIDO

V= longitud*ancho*grosor V=circunferencia del cilindro*altura*grosor

FÓRMULA DE VOLUMEN DE UN SÓLIDO

CARACTERÍSTICAS

 Característica 1.

El eje de rotación debe ser paralelo al DIFERENCIAL

 Característica 2.

Se debe de dejar en términos de la variable, dependiendo del diferencial que usemos

 Característica 3.

La integral se evaluara dependiendo del diferencial que usemos.

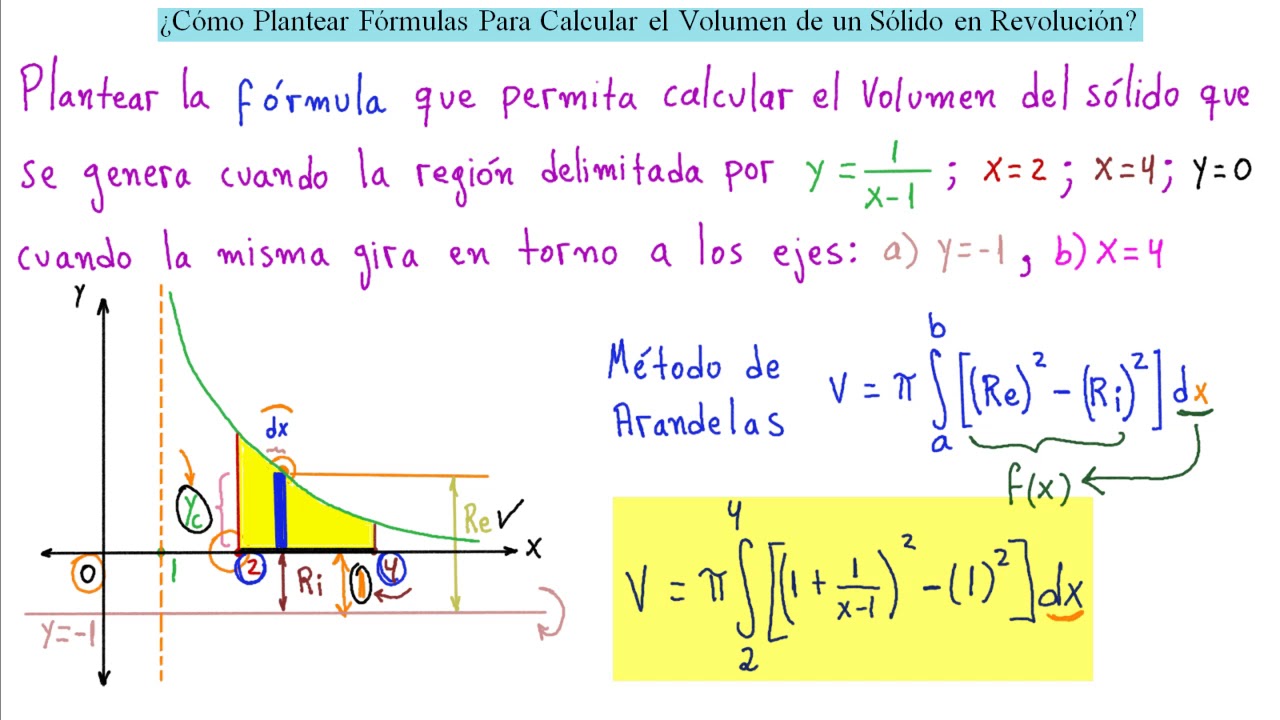
¿Cómo y Cuándo Utilizar Arandelas o Capas para Calcular Volumen?

¿Cómo y Cuándo Utilizar Arandelas o Capas para Calcular Volumen? thumbnail
 

CÁLCULO DE UN VOLUMEN CON DIFERENCIALES EN EL EJE VERTICAL

CÁLCULO DE UN VOLUMEN CON DIFERENCIALES EN EL EJE VERTICAL thumbnail
 

CÁLCULO DE UN VOLUMEN CON DIFERENCIALES EN EL EJE HORIZONTAL

CÁLCULO DE UN VOLUMEN CON DIFERENCIALES EN EL EJE HORIZONTAL thumbnail
 

ENCONTRAR EL VOLUMEN V GENERADO POR Y=X², Y=1, AL GIRAR EN Y= 2.

TAREA 15-03-2019

Usa el método de las capas cilíndricas para encontrar el volumen del sólido que se forma al girar la región en el Cuadrante I delimitada por f(x)=x−x²   y y=0  en torno a x=−1
R// El volumen del sólido es por lo tanto π/2  unidades cúbicas. 
Usa el método de las capas cilíndricas para encontrar el volumen generado al girar la región delimitada por las gráficas y= (x-1)² , y= 1; en el eje x.
R//8π /5 unidades cúbicas 
Por medio del método de los cascarones, encuentre el volumen del sólido de revolución que se forma al girar la región acotada por las gráficas y= x, x=0, y=5; en el eje x.
R//250π /3 unidades cúbicas 
Usando el método de los cascarones encuentre el volumen del sólido en revolución que se forma al girar la región acotada por las gráficas y=X² , x= 0, y= 3, primer cuadrante; eje x
R//39.17 unidades cúbicas 
Encuentre el volumen V del sólido que se forma al girar al rededor del eje y, la gráfica de y= senx² , y=0, 0≤ x ≤ √ π.
R// 2π unidades cúbicas 
Encontrar el volumen V del sólido que se forma al girar la región acotada por las gráficas de x= y² -2y  y x= 3, al rededor del la recta y= 1.
R// 8π unidades cúbicas 
Use el método de los cascarones para encontrar el volumen V del sólido que se forma al girar alrededor del eje y, la región acotada por las gráficas de y= √ x  y  y=x
R// 2π /15 unidades cúbicas 
Usando el método de los cascarones, encontrar el volumen V del sólido de revolución que se forma al girar la región acotada por las gráficas y=x² +4,   x=0,  x=2,  y=2; eje y.
R// 16π unidades cúbicas

Encontrar el volumen V que se forma al girar en el eje y,  la región acotada por las gráficas y= -x³  + 3x² ,  y=0, en el primer cuadrante.
R//243π /10 unidades cúbicas 
Encontrar por medio del método de los cascarones el volumen V del sólido de revolución que se forma al girar la región acotada por las gráficas de las ecuaciones dadas sobre el eje y. y = x²  - 2,  y= -x² + 2, x= 0, en el segundo cuadrante y tercer cuadrante.
R// 4π  unidades cúbicas

INTEGRANTES

LINDA MAYTÉ ESTRADA MORALES

Cálculo II

Carnet: 15083-18

CLAUDIA BEATRIZ MONZÓN LEMUS

Cálculo II

Carnet: 15033-16

DIEGO GUILLERMO PÉREZ RAMÍREZ

Cálculo II

Carnet: 15499-17

JONATAN MANUEL ROLDAN CASTAÑEDA

Cálculo II

Carnet: 22474-13

ESTE SITIO FUE CONSTRUIDO USANDO